Método de simplificación de Quine-McCluskey
Método de simplificación de Quine-McCluskey.
Método de Quine-McCluskey El Algoritmo Quine–McCluskey,
fue desarrollado por Willard Van Orman Quine y Edward J. McCluskeyes, para la
simplificación de funciones booleanas, similar al mapa de Karnaugh, pero
su forma tabular lo hace más eficiente para su implementación en lenguajes
computacionales.
En las matemáticas las expresiones booleanas son simplificadas por varias razones:
-Una expresión más simple es mas fácil de entender y hay menos posibilidades de que haya un error.
-Las expresiones simplificadas son mas efectivas en la práctica, como es el caso de los circuitos.
Este método es bastante útil cuando se tienen funciones con un gran número de variables, no es el caso del método de Karnaugh, que se hace
impracticable con más de cinco variables. Una expresión booleana se compone de
variables y términos. Para este método las variables sólo podrán tener un valor
numérico de cero (el correspondiente al valor de verdad false) o uno (el
correspondiente al valor de verdad true) y se designarán mediante una letra.
Metodo
Sea K un álgebra de Boole y f una función booleana
de orden n sobre K. Denotamos por B = {0, 1}. Para obtener una expresión
simplificada de f realizamos los siguientes pasos: 1. Calculamos su tabla de
verdad. 2. Ordenamos los valores cuya imagen es 1 en una columna de arriba a
abajo en número decreciente de unos. Separamos ´estos en bloques de forma que
los elementos de cada bloque tengan el mismo número de unos. 3. Comparamos cada
elemento de cada bloque con cada uno de los elementos del bloque inferior de
forma que si dos de estos elementos difieren en un único valor, les antepondremos
un + y escribiremos en una nueva columna, el elemento que se obtiene al
sustituir dicho valor por un guion. Separaremos los elementos resultantes por
una línea cuando acabemos de comparar dos bloques. 4. Repetimos el proceso
anterior con la nueva columna obtenida y así sucesivamente hasta que sólo
tengamos una única columna con un único bloque o bien, cuando de los bloques
que se tengan, no existan elementos que difieran sólo en un valor de otro
elemento del bloque siguiente. 5. Rellenamos una tabla donde escribimos en la
primera fila las secuencias de unos y ceros correspondientes a los átomos de f,
en la primera columna las secuencias con guiones que no llevan + obtenidas
anteriormente, y en cada recuadro interior correspondiente a un átomo y uno con
guión, escribiremos un asterisco si todos los valores de ambos, sin contar los
elementos con guiones coinciden. 6. Finalmente, de cada columna elegimos un
asterisco de forma que el número de filas donde hayan sido elegidos asteriscos
sea el menor posible. La suma de los elementos de la primera columna que
contienen asteriscos elegidos junto con los elementos de la primera fila en
cuya columna no hay ningún asterisco es una expresión booleana simplificada de
f.
Minimización
Se tienen dos formas de desarrollar el método de
Quine-McCluskey:con una combinación binaria y una combinación decimal.
Combinación Binaria
Sea la función: F(A, B, C, D) = Sm (1, 3, 4, 5, 7, 9, 10,
11, 15) La TABLA 1 presenta la lista de los minitérminos, expresados en forma
binaria e indica el número de UNOS que estos contienen:
A,B,C,D = 1 1 1 1 1 = 15
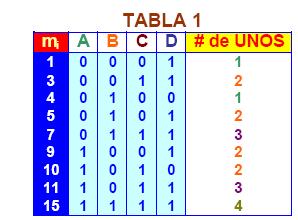
En la TABLA 2, se agrupan los minitérminos con el mismo
número de UNOS.
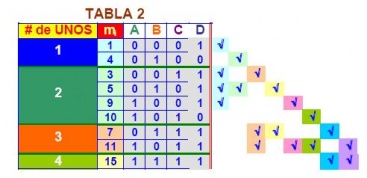
De la TABLA 2, se combinan los términos que tienen un solo
UNO con los que tienen dos UNOS, los que tienen dos UNOS con los que tienen
tres UNOS y así sucesivamente. Dos términos se podrán combinar siempre y cuando
exista un solo cambio entre ellos, es decir, cuando el lugar en que estén
colocados los UNOS coincidan. Por ejemplo, los términos 1 y 3 se combinan
debido a lo siguiente:
ABCD + ABCD = ABD(C+ C) = ABXD 0001 0011 00X1
O sea que entre los términos 1 y 3 se eliminó la variable C.
Haciendo lo mismo con los demás términos, se obtiene la TABLA 3.
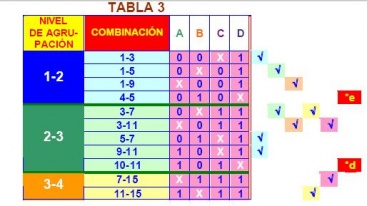
Los términos que en su fila tienen Ö, son los que se combinaron.
Los términos con *, son los que no pudieron combinarse, es decir, aquellos que
en su fila no tienen Ö. A estos términos se les denomina IMPLICANTES PRIMOS.
Para la TABLA 4, se combinan los niveles de agrupación 1-2 con 2-3 y 2-3 con
3-4, tomando en cuenta que coincidan tanto las x como los UNOS.
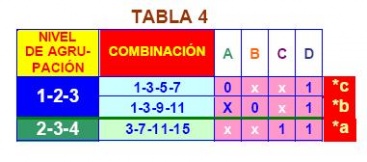
Como ya se indicó, los implicantes primos son términos que
no se combinan con ningún otro, por tanto pueden formar parte de la función
reducida.
Por tanto, la función reducida es: F(A, B, C, D) = a + b + d
+ e Donde: a= XX11= CD b= X0X1= BD d= 101X= ABC e= 010X= ABC
Finalmente, la función reducida es: F(A, B,C,D) = CD+ BD + ABC + ABC
Comentarios
Publicar un comentario